所谓二叉树,指的是 节点最多只能有 2 个子节点。一个节点可以是 0 个、1 个、最多 2 个子节点。
下图是一些二叉树的示例:

两种特殊结构的二叉树:
- 满二叉树
- 完全二叉树
满二叉树
满二叉树,是二叉树的一种特殊类型,其中每个节点要么是叶子节点,要么有两个子节点,且所有叶子节点都位于同一层。
A / \ B C / \ / \D E F G- 根节点 A 有两个子节点 B 和 C
- B 和 C 节点也有两个子节点
- D、E、F、G 就是叶子节点,并且所有的叶子节点位于同一层。
满二叉树具备如下的特点:
- 每一层的节点数:一棵满二叉树的 每一层节点数都达到了该层的最大值。对于树的第
i层(从根节点算起,根节点为第 0 层),它有2^i个节点。- 第 0 层:2^0 = 1
- 第 1 层:2^1 = 2
- 第 2 层:2^2 = 4
- 总节点数与高度的关系:如果满二叉树的高度为
h,那么它的总节点数为2^{h+1} - 1。- 第 0 层:2^1 - 1 = 1
- 第 1 层:2^2 - 1 = 3
- 第 2 层:2^3 - 1 = 7
- 叶子节点的数量:在高度为
h的满二叉树中,叶子节点 的数量为2^h。- 第 2 层:2^2 = 4
完全二叉树
另外一个用得比较多的结构是完全二叉树。
- 除了最后一层外,其他所有层都必须是满的。
- 最后一层的节点可以不满,但所有的节点必须从左到右依次排列,不允许出现中间空缺。
下面是一些完全二叉树的示例:
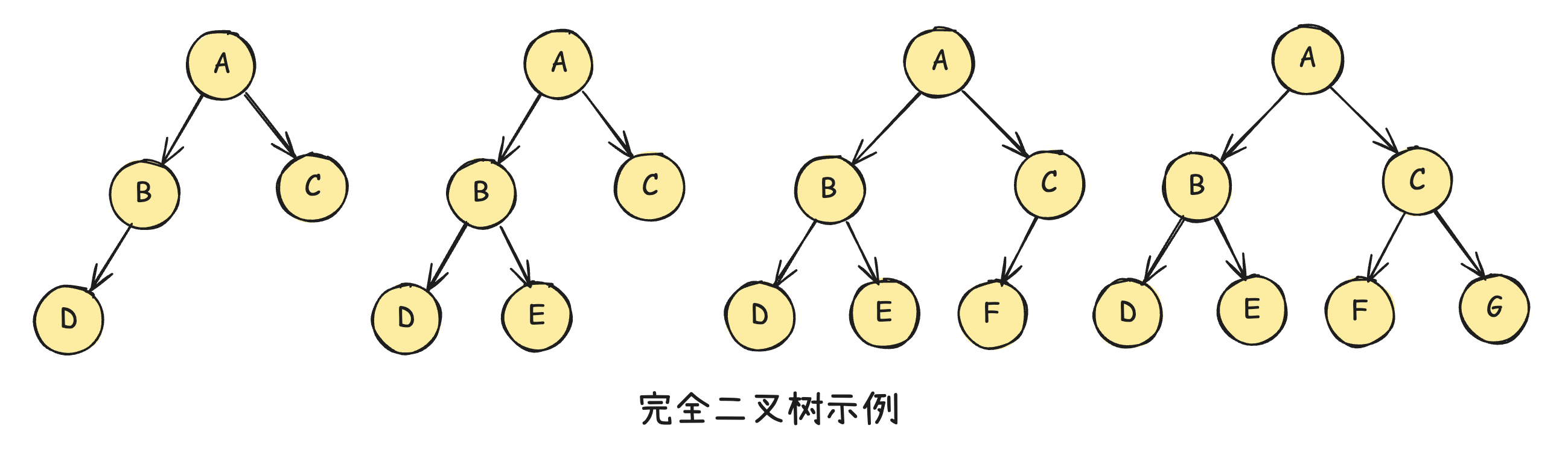
下面是一些非完全二叉树的示例:

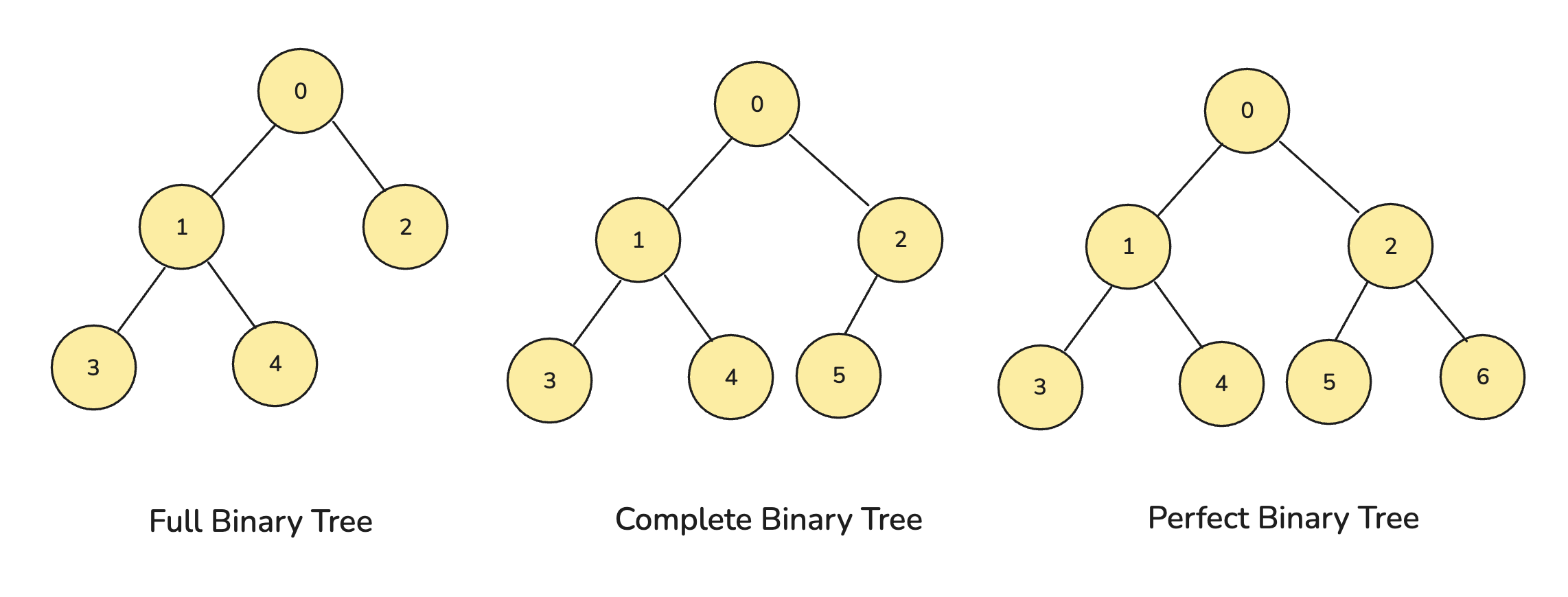
另外这里要说一个题外话,就是关于满二叉树以及完全二叉树的定义,国内和国外有一些区别。
- 完全二叉树:Complete Binary Tree
- 满二叉树:Perfect Binary Tree
- 英语中还有一个 Full Binary Tree:指的是一颗二叉树的所有节点要么没有孩子节点,要么有两个孩子节点。
二叉树特性
- 特性1:在二叉树的第 i 层最多有 2i 个节点。
A / \ B C / \ / \D E F G- 第 0 层:2^0 = 1
- 第 1 层:2^1 = 2
- 第 2 层:2^2 = 4
- 第 3 层:2 ^ 3 = 8
- 特性2:深度为 k 的二叉树,最多有 2k+1 - 1 个节点。
- 第 0 层:2^1 - 1 = 1
- 第 1 层:2^2 - 1 = 3
- 第 2 层:2^3 - 1 = 7
- 第 3 层:2^4 - 1 = 15
- 特性3:对于任何一颗二叉树,如果叶子节点的数量为 n0 ,度为 2 的节点的数量为 n2 ,两者之间的关系为 n2 + 1 = n0

- 叶子节点:H、I、J、F、G 一共有 5 个
- 度为 2 的节点:A、B、C、D 一共有 4 个
两者之间相差 1. 度为 2 例如 (A(B,C))
-
特性4:在完全二叉树中,n 个节点深度为:
假设有 10 个节点,按照完全二叉树的特性:

这颗完全二叉树的深度的计算:
这里我们可以通过推导一头一尾的节点来进行验证。
-
第 4 个节点,作为第 2 层的开始,深度为 3
-
接下来再验证最后一个节点 7,作为第 2 层的结束,深度仍然为 3
-
-EOF-