基本概念#
插入排序,对应的英语是 Insertion Sort,其核心思想类似于整理扑克牌:在手中已经排好序的牌堆中,逐张拿出未排序的牌,找到合适的位置插入进去,直到所有牌都有序为止。
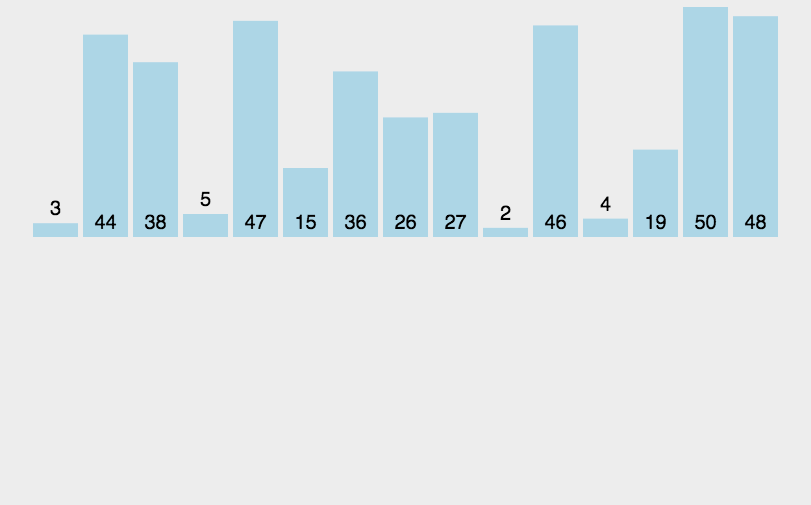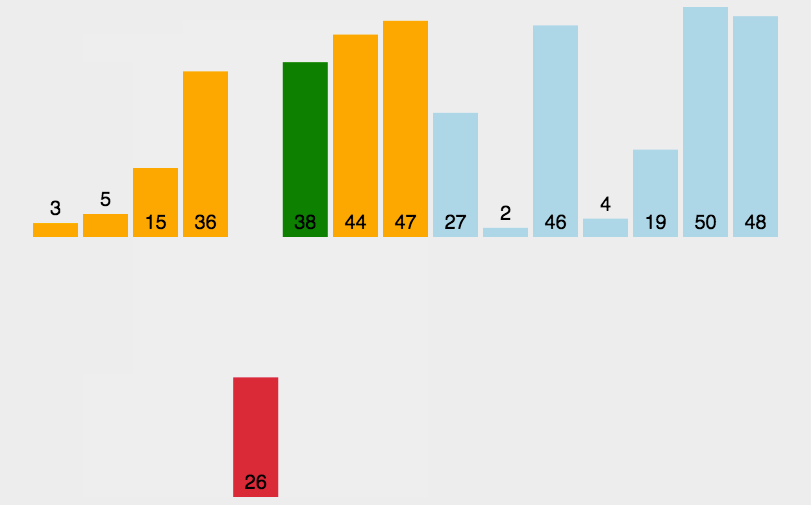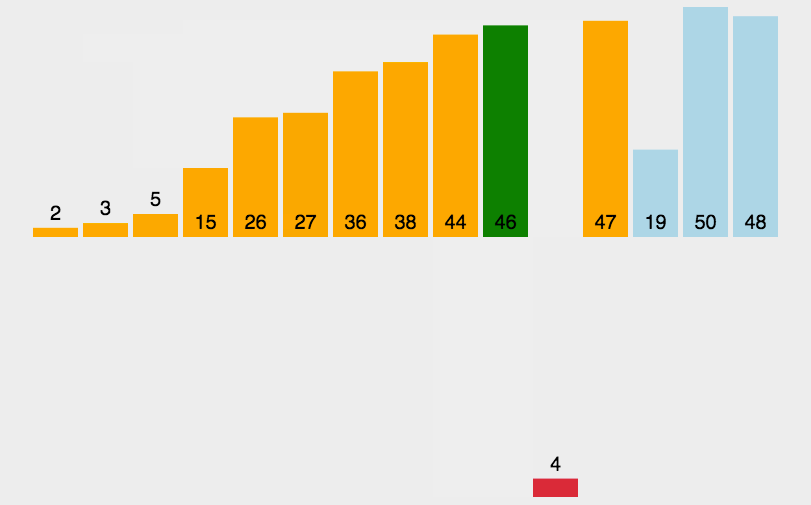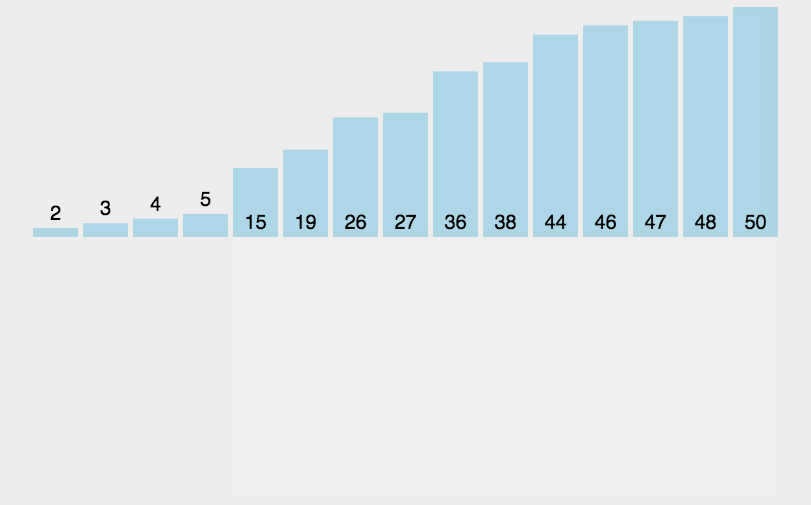
下面是插入排序的工作流程:
-
分区概念:将数组分为两个部分:已排序区间 和 未排序区间。初始时,默认第一个元素为已排序区间,其余元素为未排序区间。
-
逐个插入:从未排序区间中取出第一个元素,依次与已排序区间的元素进行比较,将其插入到合适的位置,使得已排序区间依然保持有序。
-
移动元素:当新元素小于已排序区间中的某个元素时,需要将该元素及其后续元素依次向后移动,为新元素腾出插入位置。
-
重复操作:重复以上过程,直到未排序区间为空,整个数组变成有序序列。
代码实现#
function insertionSort(arr){ // 从第二个元素开始,到最后一个元素 // 因为会假设第一个元素已经排好顺序了 for(int i = 1; i < arr.length; i++){ // 取出每一个要插入的元素 let current = arr[i];
// 要和已排序区间里面的元素进行比较,找到正确的插入位置 // j 一开始是已排序区间的最后一个元素 let j = i - 1; // 这个循环负责将已排序区间的元素往后面移动 while(j >= 0 && arr[j] > current){ arr[j+1] = arr[j]; j--; } // 跳出 while 循环的时候,说明当前元素已经找到插入的位置了 arr[j+1] = current; }}
const arr = [5, 3, 8, 4, 2];insertionSort(arr);console.log(arr);- 外层 for 循环:从第二个元素开始,将每个元素看作是待插入的元素。
- 内层 while 循环:将当前待插入的元素和已排序区间的每一个元素逐一比较,如果当前待插入元素小于已排序元素,直接将已排序元素往后移动,直到找到正确的插入位置。
复杂度#
- 时间复杂度:
O(n^2) - 空间复杂度:
O(1)
稳定性#
因为插入排序,待插入的元素只有在大于前一个数的时候,已排序区域的元素才会往后移动,值相等的话,是插入到有序数列中相同数的后面的。因此,插入排序是一种 稳定 排序。
-EOF-